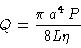Physics of Blood Flow in Small Arteries

As a complete system, the amount of blood that flows through the circulatory system is in terms of the pressure difference between the arteries and the veins times the quantity referred to as the total peripheral resistance. But what about at the local level? How much blood flows through an individual blood vessel? What are the quantities that affect the rate of blood flow? This exhibit discusses a physical relation known as Poiseuille's Law which partially answers this question.

Poiseuille's Law relates the rate at which blood flows through a small blood vessel (Q) with the difference in blood pressure at the two ends (P), the radius (a) and the length (L) of the artery, and the viscosity (n) of the blood. The law is an algebraic equation,

You can explore this law as it applies to arterioles through a number of categories, which are organized as follows:

• Historical Background of Poiseuille's Law
• Description of Parameters and Physical Conditions
• The Velocity Profile: How fast does the blood move?
• Pressure Dependence: A typical linear relation
• Viscosity Dependence: An inversely proportional relation
• Radial Dependence: A nonlinear relation
• Combined Dependence: They all work together
• Conclusions and Other Resources

  ---

  M & B Home | Previous | Next