Fourier series solutions to the wave equation on [0,1]
The wave equation can be used to model the displacement u(x,t) of a vibrating string as a function of space and time.
u_{tt}=c^2 u_{xx}
The constant c is the speed of travelling waves. The meaning of this is that if we start with function f(x) , then f(x-ct) gives a solution to the wave equation that has shape f and travels to the right with speed c .
To specify a unique solution u(x,t) to the wave equation on an interval, we must declare
- The initial position u(x,0)
- The initial velocity u_t(x,0)
- A boundary condition at each endpoint
There are many acceptable choices for boundary conditions. Here are two
- Dirichlet boundary conditions: u(0,t)=u(0,0) and u(1,t)=u(1,0)
- Neumann boundary conditions u_x(0,t)=u_x(0,0) and u_x(1,t)=u_x(1,0)
We can use Fourier series to solve the wave equation. The basic idea is that the following functions are solutions to the wave equation
\begin{array}{cc} \cos(2\pi k x)\cos(2\pi k c t), & \cos(2\pi k x)\sin(2\pi k c t), \\ \sin(2\pi k x)\cos(2\pi k c t), & \sin(2\pi k x)\sin(2\pi k c t). \end{array}
We can use Fourier series to construct a superposition of these solutions which will match our initial position and velocity.
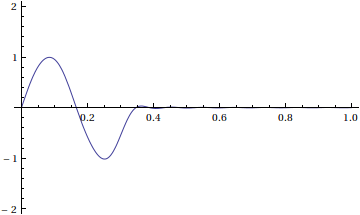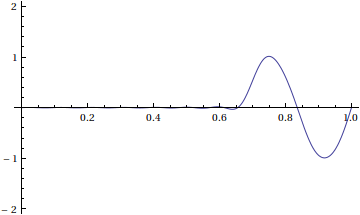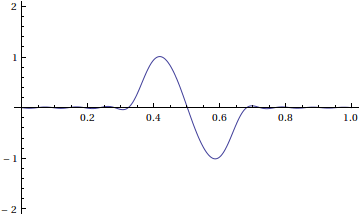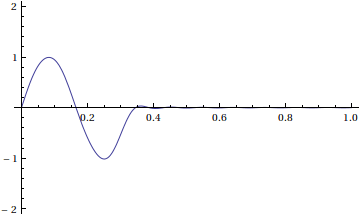
Suppose that at time t=0 , our string has the following initial position f(x) .
f(x)= \begin{cases} sin(6\pi x)&\text{ for }0\leq x\leq \frac{1}{3} \\ 0 & \text{ for }\frac{1}{3} \leq x\leq 1 \end{cases}.
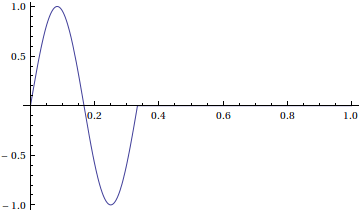
By changing the initial velocity and boundary condition, we will see that there are many possibilities for the motion of the string.
Let's start with a solution that is conceptually simple to calculate. Choose initial velocity equal to zero, and calculate a Fourier series
f(x)=\frac{a_0}{2}+\sum_{k=1}^{\infty} a_k \cos(2\pi k x)+ b_k \sin(2\pi k x)
for the 1-periodic extension of the function f(x) .
Let's choose the wave speed to be c=\frac{1}{2\pi} . Then we get the following solution to the wave equation which matches our initial position and has no initial velocity.
f(x)=\frac{a_0}{2}+\sum_{k=1}^{\infty} a_k \cos(2\pi k x)\cos(kt) + b_k \sin(2\pi k x)\cos(kt)
Here's an animation of our solution
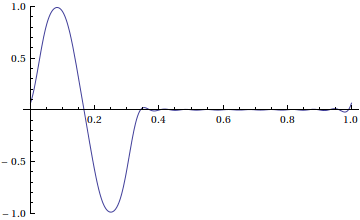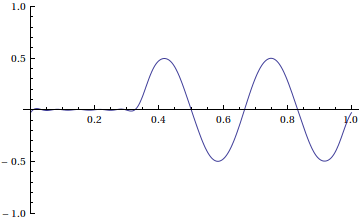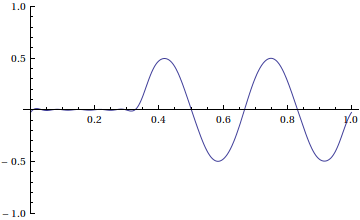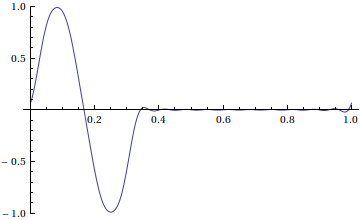
If we have in mind the motion of a vibrating string, this probably isn't what we wanted. The problem is that we didn't choose good boundary conditions-- if we are modeling the motion of a guitar string, then we need Dirichlet boundary conditions; that is, the ends of the string don't move.
To get a solution with Dirichlet boundary conditions, we need to try again using a superposition of \sin(2\pi k x) type solutions. So we need a Fourier sine series for our initial position. This is obtained by choosing the following extension of f(x) to a 2-periodic odd function.
g(x)= \begin{cases} sin(6\pi x)&\text{ for }-\frac{1}{3}\leq x\leq \frac{1}{3} \\ 0 & \text{ for }\frac{1}{3} \leq x\leq \frac{5}{3} \end{cases}.
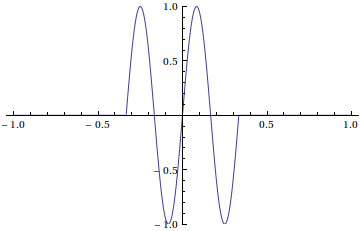
We now get the following solution with Dirichlet boundary conditions
u(x,t)=\sum_{k=1}^{\infty} b_k(g) \sin(2\pi k x)\cos(kt)
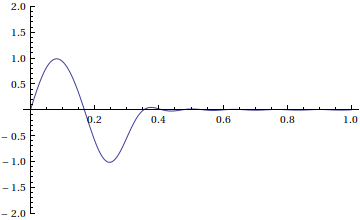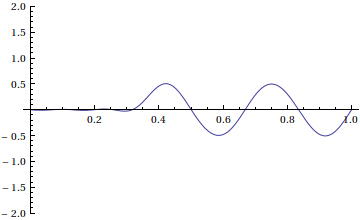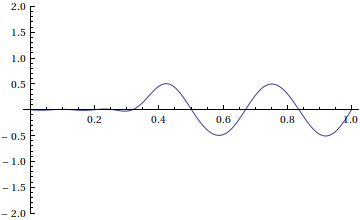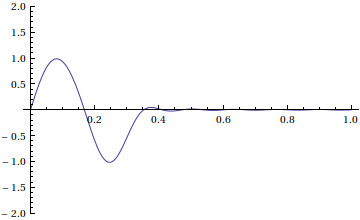
What if we want to find a solution that is a traveling wave with shape f(x) moving to the right? To make this happen, we need
\begin{array}{>{\displaystyle}l >{\displaystyle}l >{\displaystyle}l} f(x-ct)&=&u(x,t) \\ &=& \frac{a_0}{2}+\sum_{k=1}^{\infty} a_k \cos(2\pi k x)\cos(k t)+\alpha_k \sin(2\pi k x)\sin(k t)+b_k \sin(2\pi k x)\cos(k t)+\beta_k \cos(2\pi k x)\sin(k t)\end{array}
By taking a time derivative and evaluating at t=0 we see that
-cf'(x)= \sum_{k=1}^{\infty} k \alpha_k \sin(2\pi k x)+k\beta_k \cos(2\pi k x)
But differentiating the Fourier series for f(x), we have
f'(x)= \sum_{k=1}^{\infty} -2\pi k a_k \sin(2\pi k x)+2\pi k b_k \cos(2\pi k x)
We conclude that \alpha_k=2\pi c a_k = a_k, \,\,\beta_k=-2\pi c b_k =-b_k . Then our Fourier series solution is
u(x,t)= \sum_{k=1}^{\infty} a_k \left(\cos(2\pi k x)\cos(k t) +\sin(2\pi k x)\sin(k t)\right) +b_k \left(\cos(2\pi k x)\cos(k t)-\sin(2\pi k x)\sin(k t)\right)
Here is an animation of this solution using a 20-term Fourier series and frames at time steps of 0.02.
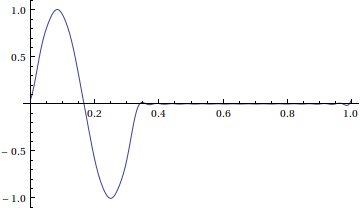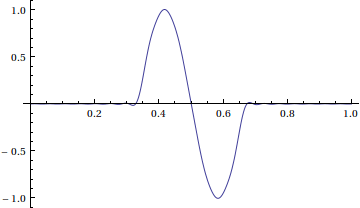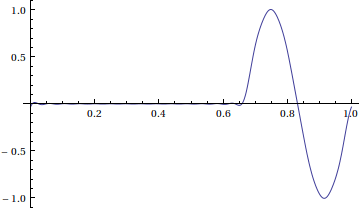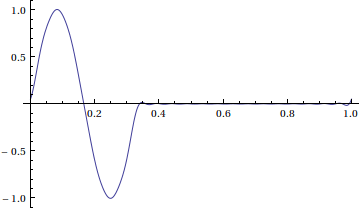
Notice that we didn't enforce Dirichlet boundary conditions. This solution represents the window [0,1] of a very long string with many waves of the shape above traveling to the right.
For one last example, let's impose Dirichlet boundary conditions on the traveling wave above. To do this we must construct the correct initial position and velocity using only functions with sine-type x-dependence.
u(x,t)= \sum_{k=1}^{\infty} \alpha_k \sin(2\pi k x)\sin(k t)+b_k \sin(2\pi k x)\cos(k t)
We already calculated the Fourier sine series for the initial position; we found that b_k=b_k(g) where g(x) is the 2-periodic odd-function extension of f(x). We now calculate the coefficients \alpha_k by differentiating the travelling wave formula with respect to time.
\begin{array}{>{\displaystyle}l >{\displaystyle}l >{\displaystyle}l} f(x-ct)&=&u(x,t) \\ &=& \sum_{k=1}^{\infty} \alpha_k \sin(2\pi k x)\sin(k t)+b_k \sin(2\pi k x)\cos(k t) \\ & & \\
-cf'(x) &=&u_t(x,0) \\ &=& \sum_{k=1}^{\infty} k \alpha_k \sin(2\pi k x) \\ & & \\-cf(x)&=&\sum_{k=1}^{\infty} \frac{ -\alpha_k}{2\pi} \cos(2\pi k x) \end{array}
Therefore the \alpha_k 's are the Fourier cosine coefficients for the function f(x) . To get these we extend to a 2-periodic even function
h(x)= \begin{cases} -\sin(6\pi x) & \text{ if }-\frac{1}{3}\leq x\leq 0 \\ \sin(6\pi x) & \text{ if }0 \leq x\leq \frac{1}{3} \\ 0 & \text{ if } \frac{1}{3}\leq x \leq \frac{5}{3} \end{cases}
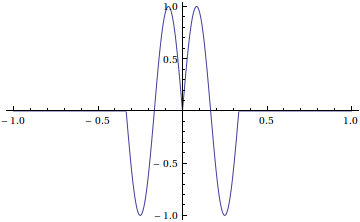
Then our solution is
u(x,t)= \sum_{k=1}^{\infty} a_k(h)sin(2\pi k x)\sin(k t)+ b_k(g) sin(2\pi k x)\cos(k t)