Poisson summation formula
The Poisson summation formula says that if you take the Fourier transform of a function, and evaluate at an integer k; then you get the kth Fourier coefficient of the periodization of f. An exact statement of the formula is
c_{k}(P_T f)= \frac{2\pi}{T}\widehat{f}\left(\frac{2\pi}{T}k\right)
where the T-periodization of f is given by
(P_T f)(t)= \sum_{m=-\infty}^\infty f(t+mT)
Shannon sampling formula
One appliction of the Poisson summation formula is to approximate a function from its values at finitely many points. This is done using the Shannon sampling theorem: If f\in L^1 (R) then you can choose any T>0 and make the following approximation
f(t)\approx \sum_{k=-\infty}^\infty f \left(k \frac{2\pi}{T}\right) \frac{\sin(Tt/2-k\pi)}{Tt/2-k\pi}.
You get a garunteed maximum error for this approximation:
\text{Error}(t)\leq 2\sqrt{2\pi}\int_{|\xi|\geq T/2} |\widehat{f}(\xi)|\, d\xi
The estimate doesn't depend on t, so this is a uniform approximation. The actual maximum error of the approximation could be less than this, but cannot be more. The parameter T tells you how close together your sample points are.
Notice that if the Fourier transform of f only takes nonzero values inside the interval [-T/2,T/2] , then the error is zero.
If you want to approximate f by calculating its values at finitely many points, then you can use a finite trunction of the sum in the approximation. The quality will of course depend on how many terms you use.
Approximation of a function using the Shannon sampling formula
Now let's take an actual function and approximate it by Shannon sampling. I picked the function to be a triangle bump of height 10 and slope \pm 1 centered at 0.
f(t)=\begin{cases} 0 &\text{ if }|t|>10 \\ 10+x & \text{ if }-10\leq x \leq 0 \\ 10-x & \text{ if }0\leq x \leq 10 \end{cases}
I used the computer program Mathematica to calculate the Fourier transform of f:
\begin{array}{rl} \widehat{f}(\xi)=& \frac{1}{2\pi}\int_{-10}^0 (10+t)e^{-i\xi t}\, dt + \frac{1}{2\pi}\int_{0}^{10} (10-t)e^{-i\xi t}\, dt \\=&\frac{1}{\sqrt{2\pi}}\frac{1}{\xi^2}e^{-10i\xi}(1-e^{10i\xi})^2 \end{array}
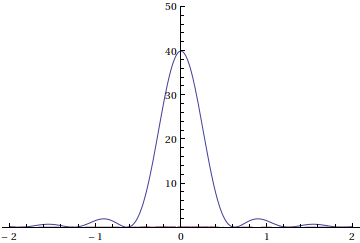
We can then approximate f with the Shannon sampling. By integrating numerically, we can calculate error estimates for different T-values
\begin{array}{cc} M & 2\sqrt{2\pi}\int_{|\xi|\geq T/2} |\widehat{f}(\xi)|\, d\xi \\ & \\ 1 & 13.2 \\ 5 & 3.20 \\ 20 & 0.809 \\ 100 & 0.0871 \end{array}
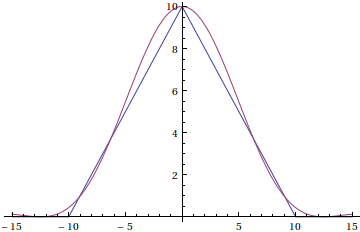
Here's an approximation with T=1. I truncated the sum at k=-3...3. The approximation is
f(t)\approx \sum_{k=-3}^{3} f \left( 2\pi k\right) \frac{\sin(t/2-k\pi)}{t/2-k\pi}
Now let's try for a better approximation; use T=20, and truncate the sum k=-20...20
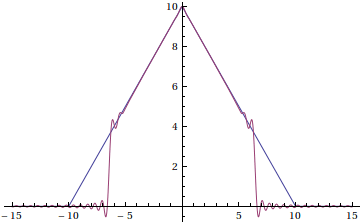
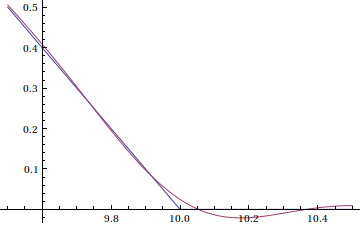
The error estimate was 0.809, but this approximation doesn't come close to that. This is because we truncated the sum too soon. If we use k=-40..40 instead, we get
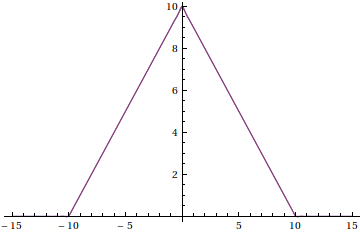
You can see that this approximation is actually much better than the error estimate garuntees. Let's zoom in on the interval from 9.5 to 10.5: