Gibbs phenomenon for the sawtooth wave
When we use Fourier series to approximate a function with jump discontinuities, we get an approximation that is not uniform near the jumps.
For example, here is a 20 term Fourier series for the sawtooth wave
f(x)=\begin{cases} \frac{-1}{2\pi}(x+\pi) & \text{ if } -\pi\leq x\leq0 \\ \frac{-1}{2\pi}(x-\pi) & \text{ if } 0\leq x\leq\pi \end{cases}
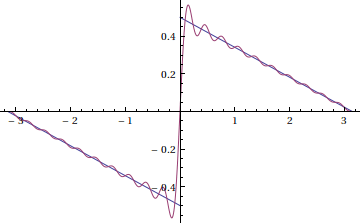
The overshoot of a function at a point is defined by
\text{Overshoot}(f;x_0):=\text{ Max}\left\{ \text{limsup}_{N\rightarrow\infty}S_N(x_N):\,\,(x_N)\text{is a sequence conv. to }x_0\right\}
It turns out that regardless of the function we are trying to approximate, the overshoot of the Fourier series at a given discontinuity is proportional to the jump there.
\text{Overshoot}(f;x_0)=\left(\frac{Si(\pi)}{\pi}-\frac{1}{2}\right)\,\text{Jump}\,(f;x_0)
Where the jump and sine integral are defined by
\begin{array}{rcl} Si(x)&=& \int_{0}^x \frac{\sin (t)}{t}\, dt \\ & & \\ \text{Jump}\,(f;x_0)&=& \text{lim}_{x\rightarrow x_0+}f(x)-\text{lim}_{x\rightarrow x_0-}f(x) \end{array}.
Here is a plot of the sine integral function
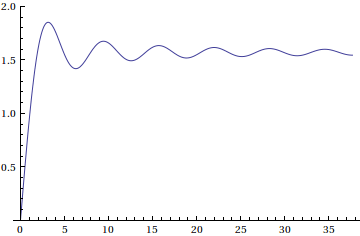
So the overshoot of a function's Fourier series at a jump of 1 is approximately 0.089489872. This can be observed in the following animation
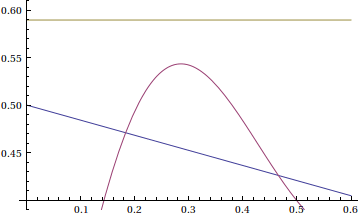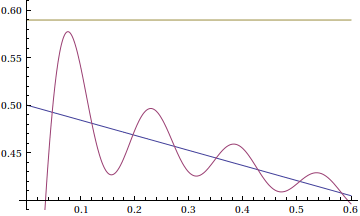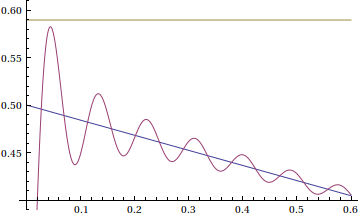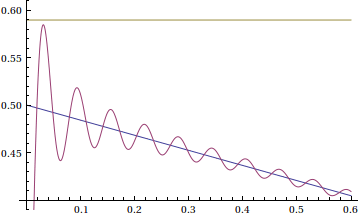
Fourier series are shown with 10,15,20,25,...,100 terms in a window near the jump discontinuity.



