Suppose f(x) and g(t) are two functions of real numbers. Their convolution is defined by

f \ast g(x)= \int_R f(x-t)g(t)\, dt
You should think of the convolution as a combination of horizontal shifts of the function f, multiplied by weights given by the values of g. Suppose we approximate the convolution using a Riemann sum:
f \ast g(x)\approx \sum_{k=-N}^N f(x-k\Delta t)g(k \Delta t)\, \Delta t
Any such approximation is a linear combination of horizontal shifts of the function f.

Let's look at an example. Here we have chosen a function f(x) that vanishes except for x values in this window.

We will convolve f with a gaussian function g(t)=2e^{-t^2/2}

First, let's look at a Riemann sum approximation of the convolution of f and g. We will use sample points at t=-2,-1,0,1,2 .

\begin{array}{ccc} t & \text{weight }g(t) & \text{shift of }f \\ & & \\ -2 & 0.2706 & f(x+2) \\ -1 & 1.2130 & f(x+1) \\ 0 & 2.0000 & f(x) \\ 1 & 1.2130 & f(x-1) \\ 2 & 0.2706 & f(x-2) \end{array}

Here is an animation of the multiples of translations of f(x) that we will add together to form our Riemann sum approximation of the convolution f \ast g (x) .

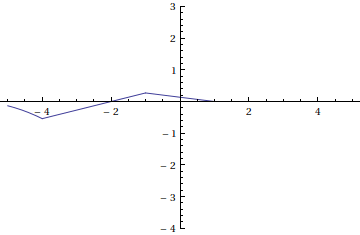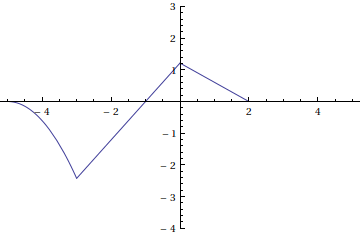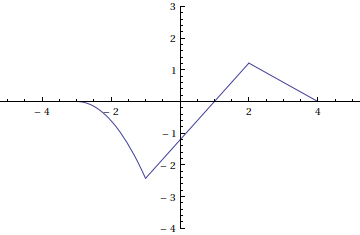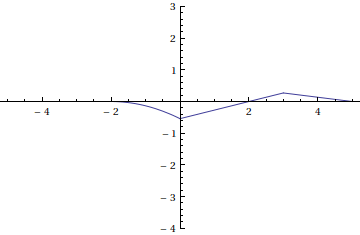
Adding the functions from each frame in the animation above gives us the following Riemann sum approximation for the convolution.

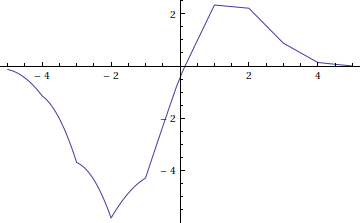
Now compare this to a true plot of the convolution f \ast g (x) .